Radian and degree measures of angles
Relation of a circle radius and a circumference
length. Table of degree and radian measures
for some most used angles.
A degree measure. Here a unit of measurement is a degree (its designation is ° or deg ) – a turn of a ray by the 1 / 360 part of the one complete revolution. So, the complete revolution of a ray is equal to 360 deg. One degree is divided into 60 minutes (a designation is ‘ or min ); one minute – correspondingly into 60 seconds (a designation is “ or sec ) .
A radian measure.
As we know from plane geometry (
see
the point "A length of arc" of the paragraph "Geometric locus. Circle and circumference"
), a length of an arc
l ,
a radius
r
and a corresponding central angle
are tied by the relation:
= l / r .
This formula is a base for definition of a
radian measure
of angles. So, if
l
=
r ,
then
= 1, and we say, that an angle
is equal to1 radian, that is designed as
= 1
rad
. Thus, we have the following definition of a radian measure unit:
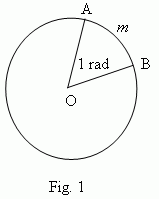
A radian is a central angle, for which lengths of its arc and radius are equal ( A m B = AO, Fig.1 ). So, a radian measure of any angle is a ratio of a length of an arc drawn by an arbitrary radius and concluded between sides of this angle to the arc radius.
Following this formula, a length of a circumference C and its radius r can be expressed as:
=
C / r .
So
,
a round angle, equal to 360° in a degree measure, is simultaneously
2
in a radian measure. Hence, we receive a value of one radian:
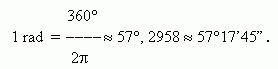
Inversely,
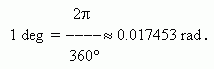
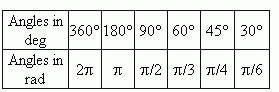
It is useful to remember the following comparative table of degree and radian measure for some angles, we often deal with:
