Geometrical locus. Circle and circumference

Geometrical locus ( or simply locus ) is a totality of all points, satisfying the certain given conditions.

E x a m p l e 1. A midperpendicular of any segment is a locus, i.e. a totality of all points, equally
removed from the bounds of the segment. Suppose that  PO AB and  AO = OB :

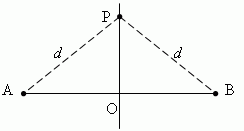
Then, distances from any point P, lying on the midperpendicular PO, to bounds A and B of the segment AB are both equal to d . So, each point of a midperpendicular has the following property:  it is removed from the bounds of the segment at equal distances.

E x a m p l e 2. An

E x a m p l e 3. A circumference is a locus, that is a totality of all points ( one of them - A ),
equally removed from its center O.

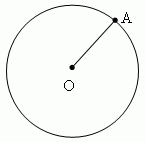
Circumference is a geometrical locus in a plane, that is a totality of all points, equally removed from its center. Each of the equal segments, joining the center with any point of a circumference is called a radius and signed as r or R . A part of a plane inside of a circumference, is called a circle . A part of a circumference ( for instance, A m B,  Fig.39 ) is called an arc of a circle. The straight line PQ, going through two points M and N of a circumference, is called a secant ( or transversal ). Its segment MN, lying inside of the circumference, is called a chord.

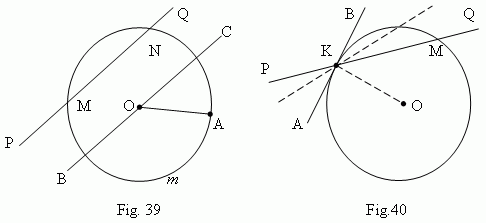
A chord, going through a center of a circle ( for instance, BC, Fig.39 ), is called a diameter and signed as d or D . A diameter is the greatest chord of a circle and equal to two radii ( d = 2 r ).

Tangent. Assume, that the secant PQ ( Fig.40 ) is going through points K and M of a circumference. Assume also, that point M is moving along the circumference, approaching the point K. Then the secant PQ will change its position, rotating around the point K. As approaching the point M to the point K, the secant PQ  tends to some limit position  AB. The straight line AB is called a tangent line or simply a tangent to the circumference in the point K. The point K is called a point of tangency. A tangent line and a circumference have only one common point – a point of tangency.

Properties of tangent.

1) A tangent to a circumference is perpendicular to a radius, drawing to a point of
tangency ( AB OK,  Fig.40 ) .

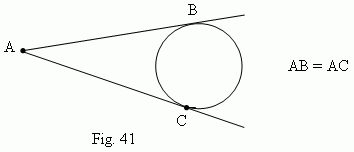
2) From a point, lying outside a circle, it can be drawn two tangents to the same
circumference; their segments lengths are equal ( Fig.41 ).

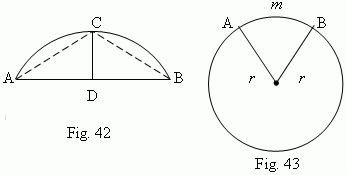
Segment of a circle is a part of a circle, bounded by the arc ACB and the corresponding chord AB ( Fig.42 ). A length of the perpendicular CD, drawn from a midpoint of the chord AB until intersecting with the arc ACB, is called a height of a circle segment. Sector of a circle is a part of a circle, bounded by the arc A m B and two radii OA and OB, drawn to the ends of the arc ( Fig.43 ).

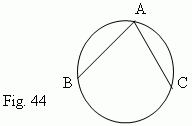
Angles in a circle. A central angle – an angle, formed by two radii of the circle ( AOB, Fig.43 ).  An inscribed angle – an angle, formed by two chords AB and AC, drawn from one common point ( BAC, Fig.44 ).

A circumscribed angle – an angle, formed by two tangents AB and AC, drawn from one common point  ( BAC, Fig.41 ).
A length of arc of a circle is proportional to its radius r and  the corresponding central angle :

l = r

So, if we know an arc length l and a radius r , then the value of the corresponding central angle can be determined as their ratio:

= l / r .

This formula is a base for definition of a radian measure of angles. So, if l = r, then = 1,  and we say, that an angle is equal to 1 radian  ( it is designed as = 1 rad ). Thus, we have the following definition of a radian measure unit: A radian is a central angle ( AOB, Fig.43 ), whose arc’s length is equal to its radius ( AmB = AO, Fig.43 ). So, a radian measure of any angle is a ratio of a length of an arc, drawn by an arbitrary radius and concluded between the sides of this angle, to the radius of the arc. Particularly, according to the formula for a length of an arc, a length of a circumference C can be expressed as:

C = 2 r ,

where is determined as ratio of C and a diameter of a circle  2 r :

= C / 2 r .

is an irrational number; its approximate value is 3.1415926…
On the other hand, 2 is a round angle of a circumference, which in a degree measure is equal to 360 deg. In practice it often occurs, that both radius and angle of a circle are unknown. In this case, an arc length can be calculated by the approximate Huygens’ formula:

p 2 l + ( 2 l – L ) / 3 ,

where ( according to Fig.42 ): p – a length of the arc ACB; l – a length of the chord AC;
L – a length of the chord AB. If an arc contains not more than 60 deg, a relative error of this formula is less than 0.5%.

Relations  between  elements  of a circle. An  inscribed  angle (

ABC

AOC

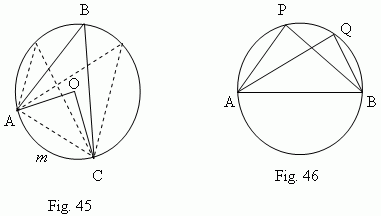
All inscribed angles, based on a semi-circle ( APB, AQB, …,  Fig.46 ), are right angles ( Prove this, please ! ). An angle ( AOD,  Fig.47 ), formed by two chords ( AB and CD ), is measured by a semi-sum of arcs, concluded between its sides:
( A n D + C m B ) / 2 .

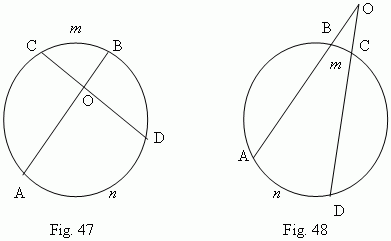
An angle ( AOD, Fig.48 ) , formed by two secants ( AO and OD ), is measured by a semi-difference of arcs, concluded between its sides: ( A n D – B m C ) / 2 . An angle ( DCB,  Fig.49 ) , formed by a tangent and a chord ( AB and CD ), is measured by a half of an arc, concluded inside of  it: C m D  / 2 . An angle ( BOC,  Fig.50 ) , formed by a tangent and a secant ( CO and BO ), is measured by a semi-difference of arcs, concluded between its sides: ( B m C – C n D ) / 2 .

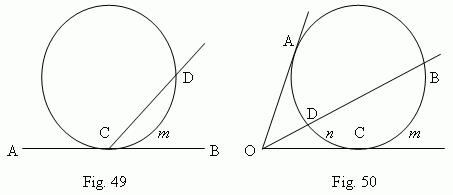
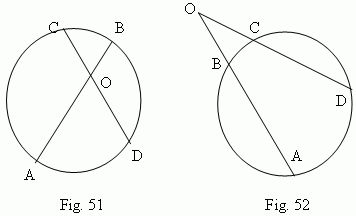
A circumscribed angle ( AOC, Fig.50 ) , formed by the two tangents, (CO and AO), is measured by a semi-difference of arcs, concluded between its sides: ( ABC – CDA ) / 2 . Products of segments of chords ( AB and CD,  Fig.51 or  Fig.52 ), into which they are divided by an intersection point, are equal: AO · BO = CO · DO.

A

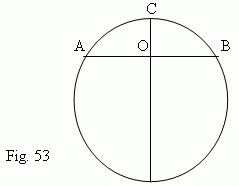
A chord ( AB, Fig.53 ) , which is perpendicular to a diameter ( CD ) , is divided into two in the intersection point O :
AO = OB . ( Try to prove this ! ).