Elementary functions and their graphs
Hyperbola. Quadratic function. Quadratic parabola.
Power function. Cubic parabola. Exponential function.
Logarithmic function. Trigonometric functions. Sinusoid.
Intervals of monotony. Inverse trigonometric functions.
| 1. |
Proportional values.
If variables
y
and
x
are
direct proportional
, then the functionaldependence between them is represented by the equation:
where k is a constant a factor of proportionality . A graph of a direct proportionality is a straight line, going through an origin of coordinatesand forming with an x -axis an angle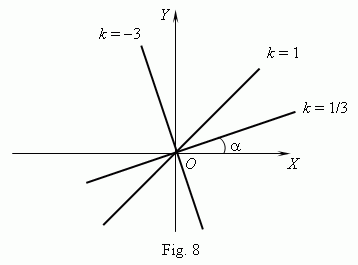 
, a tangent of which is equal to
k
: tan
=
k
( Fig.8 ). Therefore, a factor of proportionality is called also a
slope
. There are shown three graphswith
k
= 1/3,
k
= 1 and
k
= – 3 on Fig.8.
|
| 2. |
Linear function.
If variables
y
and
x
are
tied by the 1-st degree equation:
( at least one of numbers A or B is non-zero ), then a graph of the functional dependence is a straight line. If C = 0, then it goes through an origin of coordinates, otherwise - not.Graphs of linear functions for different combinations of A, B, C are represented on Fig.9.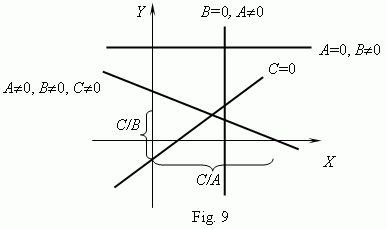 
|
| 3. |
Inverse proportionality.
If variables
y
and
x
are
inverse proportional
, then the functionaldependence between them is represented by the equation:
where k is a constant. A graph of an inverse proportionality is a curve, having two branches ( Fig.10 ). This curveis called a hyperbola . These curves are received at crossing a circular cone by a plane(about conic sections see the paragraph "Cone" in the part "Stereometry (Solid geometry)" ).As shown on Fig.10, a product of coordinates of a hyperbola points is a constant value, equal in this case to 1. In general case this value is k , as it follows from a hyperbola equation: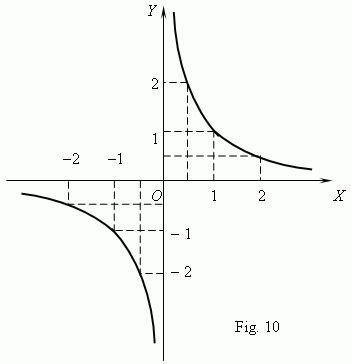 
The main characteristics and properties of hyperbola:
|
| 4. |
Quadratic function.
This is the function:
y
=
ax
2
+
bx
+
c
, where
a, b, c
–
constants,
a
0. In the simplest case we have
b
=
c
= 0 and
y
=
ax
2
. A graph of this function is a
quadratic
parabola
- a curve, going through an origin of coordinates ( Fig.11 ). Every parabola has an axis of symmetry
OY
, which is called an
axis of parabola.
The point
O
of intersection of a parabola with its axis is a
vertex of parabola.
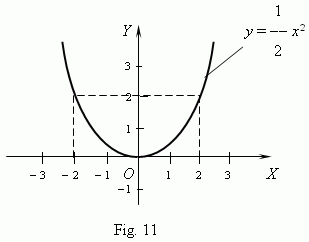
A graph of the function y = ax 2 + bx + c is also a quadratic parabola of the same shape, that y = ax 2 , but its vertex is not an origin of coordinates, this is a point with coordinates:
|
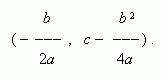
The form and location of a quadratic parabola in a coordinate system depends completely on two parameters: the
coefficient
a
of
x
2
and
discriminant D = b
2
–
4
ac
. These properties follow from analysis of the quadratic equation roots ( see
the corresponding paragraph in the part "Algebra"
).
All possible different cases for a
quadratic parabola are shown on Fig.12.
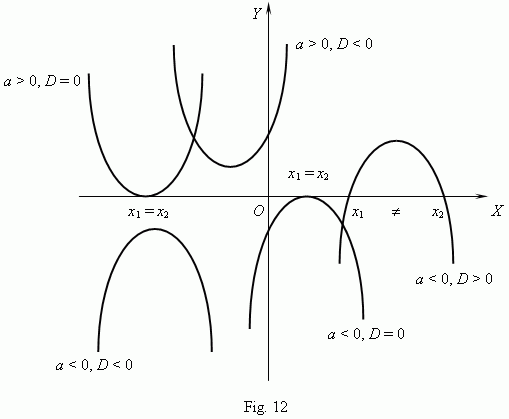
Show, please, a quadratic parabola for the case a > 0, D > 0 .
The main characteristics and properties of a
quadratic parabola:
- the function domain:
–
<
x
< +
( i.e.
x
is any real number ) and codomain:
…
( answer, please, this question yourself !) ;
-
the function is not monotone on the whole, but to the right or to the left of the vertex it
behaves as a
monotone function;
- the function is unbounded, continuous in everywhere, even at
b
=
c
= 0, and non-periodic;
- the function has no zeros at
D
< 0. ( What about this at
D
0 ? ) .
| 5. |
Power function.
This is the function:
y = ax
n
where
a, n
– constants. At
n
= 1 we receive the function, called a
direct proportionality
:
y =
ax
; at
n
= 2 - a
quadratic
parabola
; at
n
= – 1 - an
inverse proportionality
or
hyperbola.
So, these functions are particular casesof a power function. We know, that a zero power of every non-zero
number is 1, thus at
n
= 0 the power function becomes a constant:
y = a
, i.e. its graph is a straight line, parallelto an
x
-axis, except an origin of coordinates ( explain, please, why ? ).All these cases (at
a
= 1 ) are shown on Fig.13 (
n
0 ) and Fig.14 (
n
< 0 ) .Negative values of
x
are not considered here, because then some of functions:
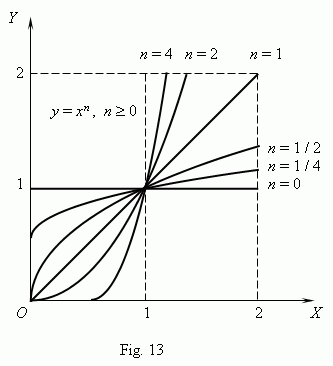
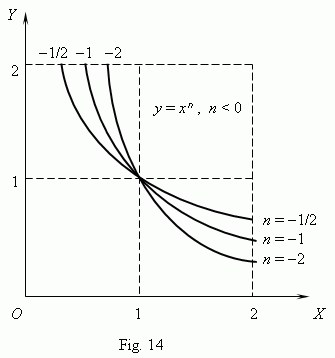
If n – integer, power functions have a meaning also at x < 0, but their graphs have different forms depending on that is n an even or an odd number. On Fig.15 two such power functions are shown: for n = 2 and n = 3.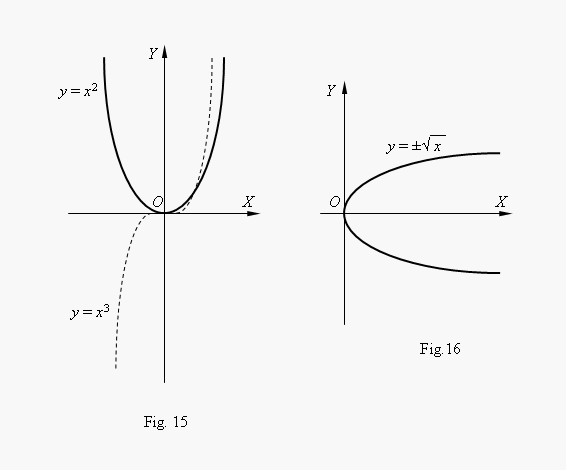 
At n = 2 the function is even and its graph is symmetric relatively an axis Y ; at n = 3 the function is odd and its graph is symmetric relatively an origin of coordinates. The function y = x 3 is called a cubic parabola. On Fig.16 the function 
is represented. This function is inverse to the quadratic parabola
y
=
x
2
, its graph is received by rotating the quadratic parabola graph around abisector of the 1-st
coordinate angle. (This is the way to receive a graph of every inverse function from its original function). We see by the graph, that this is the
two-valued function(the sign ± before the square root symbol says about this). Such functions are not studied in an elementary mathematics, therefore
we consider usually as a function one of its branches: either an upper or a lower branch.
|
| 6. |
Exponential function.
The function
y
=
a
x
, where
a
is a positive constant number, is called an
exponential function.
The argument
x
adopts
any real
values; as the
function values
only positive numbers
are considered, because otherwise we'll have a multi-valued function. So, the function
y
= 81
x
has at
x
= 1/4 four different values:
y
= 3,
y
= – 3,
y
= 3
i
and
y
= – 3
i
( check this, please ! ). But we consider as the function value only
y
= 3. Graphs of an exponential
function for
a
= 2 and
a
= 1 / 2 are shown on Fig.17. All they are goingthrough the point ( 0, 1 ). At
a
= 1 we have as a graph a straight line, parallel to
x
-axis,i.e. the function becomes a constant value, equal to 1. At
a
> 1 an exponential function increases, and at 0 <
a
< 1 – decreases.
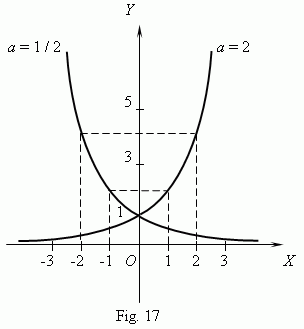
The main characteristics and properties of a exponential function: - the function domain: –
<
x
<
+
( i.e.
x
is any real number ) and its codomain:
y
>
0;
- this is a monotone function: it increases at a > 1 and decreases at 0 < a < 1; - the function is unbounded, continuous in everywhere, non-periodic; - the function has no zeros.
|
| 7. |
Logarithmic function.
The function
y
= log
a
x
, where
a
is a positive constant number,not equal to 1, is called a
logarithmic function
. This is an inverse function relatively to anexponential function; its graph ( Fig.18 ) can be
received by rotating a graph of an exponential function around of a bisector of the 1-st coordinate angle.
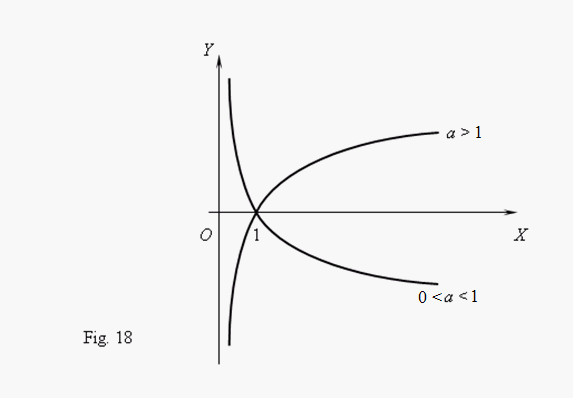
The main characteristics and properties of a logarithmic function: - the function domain: x > 0 and its codomain: –
<
y
<
+
(
i.e.
y
is
any
real number
);
- this is a monotone function: it increases at a > 1 and decreases at 0 < a < 1; - the function is unbounded, continuous in everywhere, non-periodic; - the function has one zero: x = 1. |
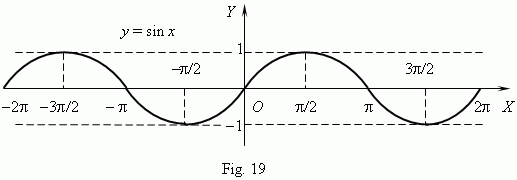
| 8. | Trigonometric functions. Building trigonometric functions we use a radian as a measure of angles. Then the function y = sin x is represented by the graph ( Fig.19 ). This curve iscalled a sinusoid . |
The graph of the function
y
= cos
x
is represented on Fig.20 ; this is
also a sinusoid,
received from the graph of
y
= sin
x
by its moving along an
x
-axis to the left
for
/ 2.
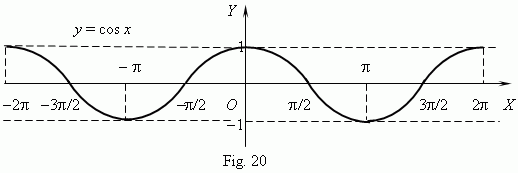
From these graphs the following main characteristics and properties of the
functions are obvious:
- the functions have as a domain:
–
<
x
< +
and a codomain: – 1
y
+1;
- these are periodic functions: their period is 2
;
- the functions are bounded (
|
y
|
1
),
continuous in everywhere; they are not monotone
functions,
but
there are
so
called
intervals of monotony
,
inside
of
which
they
behave
as
monotone functions (
see graphs Fig.19 and Fig.20
);
- the
functions
have
an
innumerable
set
of zeros( see in details
the section "Trigonometric
equations"
).
Graphs of functions y = tan x and y = cot x are shown on Fig. 21 and Fig. 22 correspondingly.
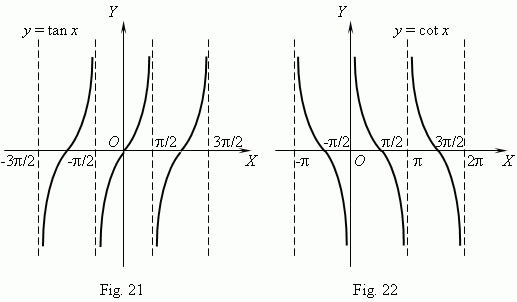
The graphs show, that these functions are: periodic (their period is
), unbounded, not monotone on the whole, but they have the intervals of monotony
(what intervals ?), discontinuous functions (what points of discontinuity these functions have ?). The domain and codomain of these functions:
