Properties of roots of a quadratic equation. Viete’s theorem
The formula
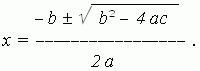
shows, that the three cases are possible:
1) b 2 – 4 a c > 0 , then two roots are different real numbers;
2) b 2 – 4 a c = 0 , then two roots are equal real numbers;
3) b 2 – 4 a c < 0 , then two roots are imaginary numbers.
The expression b 2 – 4 a c , value of which permits to differ these three cases, is called a discriminant of a quadratic equation and marked as D .
Viete’s theorem. A sum of roots of reduced quadratic equation x 2 + px + q = 0 is equal to coefficient at the first power of unknown, taken with a back sign, i.e.
x 1 + x 2 = – p ,
and a product of the roots is equal to a free term, i.e.
x 1 · x 2 = q .
To prove Viete’s theorem, use the formula, by which roots of reduced quadratic equation are calculated.