Polygon
Polygon. Vertices, angles, diagonals, sides of a polygon.
Perimeter of a polygon. Simple polygons. Convex polygon.
Sum of interior angles in a convex polygon.
A plane figure, formed by closed chain of segments, is called a
polygon
. Depending on a quantity of angles a polygon
can be a
triangle
, a
quadrangle
, a
pentagon
, a
hexagon
etc.
On Fig.17 the hexagon ABCDEF is
shown. Points
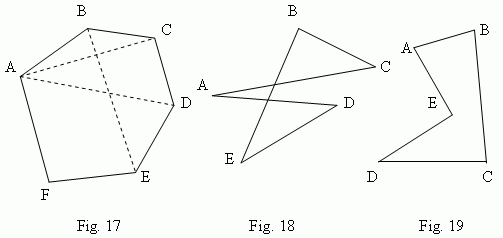
A, B, C, D, E, F –
vertices of polygon
; angles
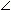 A ,
A ,
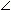 B ,
B ,
 C ,
C ,
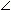 D,
D,
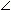 E ,
E ,
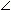 F –
angles of polygon
; segments AC, AD, BE etc. are
diagonals
; AB, BC, CD, DE, EF, FA –
sides of polygon
; a sum of
sides lengths AB + BC + … + FA is called a perimeter of polygon and signed as
p
(sometimes – 2
p
, then
p
– a half-perimeter). We consider only
simple
polygons in an elementary geometry, contours of which have no self-intersections ( as shown on
Fig.18 ). If all diagonals lie inside of a polygon, it is called a
convex
polygon. A hexagon on Fig.17 is a convex one;
a pentagon ABCDE on Fig.19 is not a convex polygon, because its diagonal AD lies outside of it. A sum of interior angles
in any convex polygon is equal to 180 (
n
– 2 ) deg, where
n
is a number of angles (or sides) of a polygon.
F –
angles of polygon
; segments AC, AD, BE etc. are
diagonals
; AB, BC, CD, DE, EF, FA –
sides of polygon
; a sum of
sides lengths AB + BC + … + FA is called a perimeter of polygon and signed as
p
(sometimes – 2
p
, then
p
– a half-perimeter). We consider only
simple
polygons in an elementary geometry, contours of which have no self-intersections ( as shown on
Fig.18 ). If all diagonals lie inside of a polygon, it is called a
convex
polygon. A hexagon on Fig.17 is a convex one;
a pentagon ABCDE on Fig.19 is not a convex polygon, because its diagonal AD lies outside of it. A sum of interior angles
in any convex polygon is equal to 180 (
n
– 2 ) deg, where
n
is a number of angles (or sides) of a polygon.
Back
