Ball (sphere)

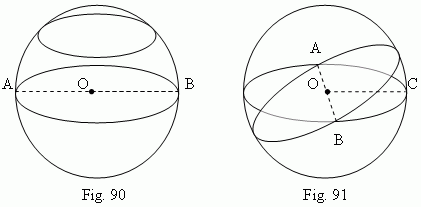
Spherical surface is a geometrical locus in a space, that is a totality of all points, equally removed from one point O, which is called a center ( Fig.90 ) . Radius AO and diameter AB are defined as well as in a circumference.

Ball (sphere) is a body, bounded by a spherical surface. It is possible to receive a ball, rotating a half-circle (or a circle) about its diameter. All plane sections of a ball – circles (Fig.90). The largest circle is in a section, going through a center of a ball and is called a large circle . Its radius is equal to a radius of a ball. Any two large circles are intersected along a diameter of a ball  (AB,  Fig.91). This diameter is also a diameter for each of these intersecting circles. Through two points of a spherical surface, placed on the ends of the same diameter (A and B, Fig.91 ), it is possible to draw an innumerable set of large circles. For instance, through the poles of Earth it is possible to draw an infinite number of meridians.

A volume of a ball is less than a volume of a curcumscribed cylinder ( Fig.92 ) in one and a half times; and a surface of a ball is less than a full surface of this cylinder also in one and a half times  (Archimedean theorem ):

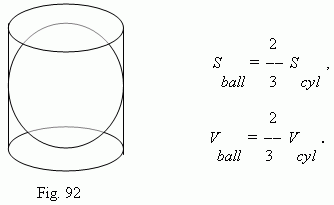
Here S _ball and V _ball - a surface and a volume of a ball correspondingly;

S _cyl and V _cyl - a full surface and a volume of a circumscribed cylinder.

Parts of a ball. A part of a ball (sphere), cut out by any plane ( ABC,  Fig.93 ), is called a spherical segment . The circle ABC is called a base of a spherical segment. The segment MN of a perpendicular, drawn from a center  N  of the circle  ABC  till intersection with a spherical surface, is called a height of a spherical segment. The point  M  is called a vertex of a spherical segment.

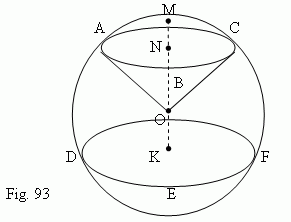
A part of a sphere, concluded between the two parallel planes ABC and DEF, crossing the spherical surface ( Fig.93 ), is called a spherical layer ; a curved surface of a spherical layer is called a spherical zone. Circles ABC and DEF  are called bases of a spherical zone. The distance NK between the bases of a spherical zone is its height .
A part of a ball, bounded by a curved surface of a spherical segment ( AMCB,  Fig.93 ) and the conic surface OABC, a base of  which is a base of a segment  ( ABC ), and a vertex – a center of a ball  O, is called a spherical sector .