Polyhedrons. Prism, parallelepiped, pyramid

Polyhedron is a body, boundary of which consists of pieces of planes (polygons). These polygons are called faces , their sides – edges , their vertices – vertices of polyhedron. Segments, joining two vertices, which are not placed on the same face, are called diagonals of polyhedron. A polyhedron is called a convex one, if all its diagonals are placed inside of it.

Prism is a polyhedron ( Fig.79 ), two faces of which ABCDE and abcde ( bases of prism ) are equal polygons with correspondingly parallel sides, and the rest of the faces (A ab B, B bc C etc.) are parallelograms, planes of which are parallel  to a straight line (A a , or B b , or C c etc.). Parallelograms A ab B, B bc C etc. are called lateral faces ;  edges A a , B b , C c etc. are called lateral edges. A height of prism is any perpendicular, drawn from any point of one base to a plane  of another base. Depending on a form of polygon in a base, the prism can be correspondingly: triangular, quadrangular, pentagonal, hexagonal and so on. If lateral edges of a prism are perpendicular to a base plane, this prism is a right prism ; otherwise it is an oblique prism . If a base of a right prism is a regular polygon, this prism is also called a regular one. On Fig.79 an oblique pentagonal prism is shown.

Parallelepiped is a prism, bases of which are parallelograms. So, a parallelepiped has six faces and all of them are parallelograms. Opposite faces are two by  two equal and parallel. A parallelepiped has four diagonals; they all intersect in the one point and they are divided in it into two. If four lateral faces of parallelepiped are rectangles, it is called a right parallelepiped. A right parallelepiped, all six faces of which are rectangles, is called a right-angled parallelepiped. A diagonal of right-angled parallelepiped d and its edges a, b, c are tied by the relation: d ² = a ² + b ² + c ² . A right-angled parallelepiped, all faces of which are squares, is called a cube . All edges of a cube are equal.

Pyramid is a polyhedron, one face of which ( a base of pyramid ) is an arbitrary polygon ( ABCDE,  Fig.80 ), and all the rest of the faces ( lateral faces ) are triangles with a common vertex  S, called a vertex of a pyramid . The perpendicular SO, drawn from a vertex of a pyramid to its base, is called a height of pyramid . Depending on a form of polygon in a base, the pyramid can be correspondingly: triangular, quadrangular, pentagonal, hexagonal and so on. A triangular pyramid is a tetrahedron, a quadrangular one – a pentahedron etc. A pyramid is called a regular one, if its base is a regular polygon and its height falls into a center of a base. All lateral edges of a regular pyramid are equal; all lateral faces are equal isosceles triangles. A height of lateral face ( SF ) is called an apothem of a regular pyramid.

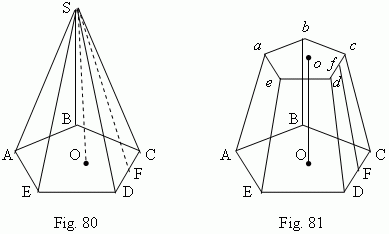
If to draw the section abcde , parallel to the base ABCDE ( Fig.81 ) of the pyramid, then a body, concluded between these planes and lateral surface, is called a truncated pyramid. Parallel faces ABCDE  and abcde are called its bases ; a distance O o between them is a height . A truncated pyramid is called a regular one, if a pyramid, from which it was received, is regular. All lateral faces of a regular truncated pyramid are equal isosceles trapezoids. The height  F f of a lateral face ( Fig.81 ) is called an apothem of a regular truncated pyramid.