Common notions

Stereometry studies geometric properties of solid bodies and figures. As well as in planimetry the basic elements are a point and a straight line , in stereometry a plane and a straight line are the basic notions. The main axiom of stereometry: Through any three points of a space, not placed on the same straight line, it is possible to draw one and only one plane. Through three points which are placed on the same line, it is possible to draw innumerable set of planes, forming in this case a pencil of planes . The straight line, through which all planes of the pencil are going, is called an axis of a pencil . Through any straight line and a point, placed outside of the line, it is possible to draw one and only one plane. It is not always possible to draw a plane through two straight lines. If it is impossible, then these straight lines are called crossing straight lines.

E x a m p l e . A horizontal straight line, drawn on one wall of a room and a vertical straight
line on an opposite wall are crossing straight lines.

Crossing straight lines don’t intersect however long they may be continued, but they are not parallel straight lines, because they don’t lie in the same plane. Parallel straight lines are the only non-intersecting lines, through which it is possible to draw a plane. The difference between crossing and parallel straight lines is that two parallel lines have the same direction, but crossing lines have not. Through two intersecting straight lines it is always possible to draw one and only one plane. A distance between two crossing straight lines is a length of the segment AB, joining the nearest points A and B ( Fig.69 ), placed on the crossing straight lines. The straight line AB is perpendicular to both of the crossing straight lines.

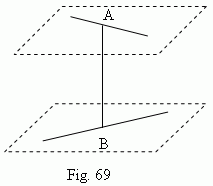
A distance between two parallel straight lines is determined as in planimetry. A distance between intersecting straight lines is adopted equal to zero. Two planes are either intersected  (along a straight line) or aren’t. Non-intersecting planes are called parallel planes . A plane and a straight line are also either intersected  ( in one point ) or aren’t. In the last case we say, that a straight line and a plane are parallel one to another.