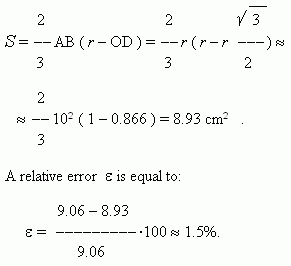Areas of plane figures

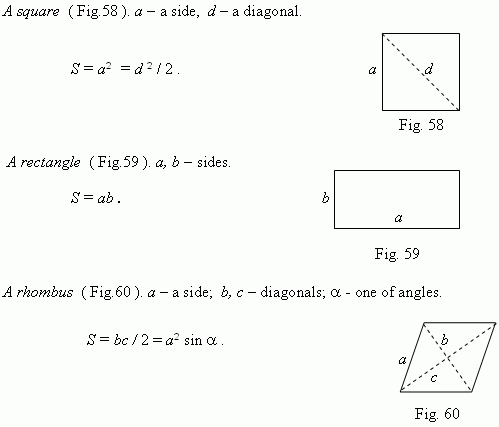
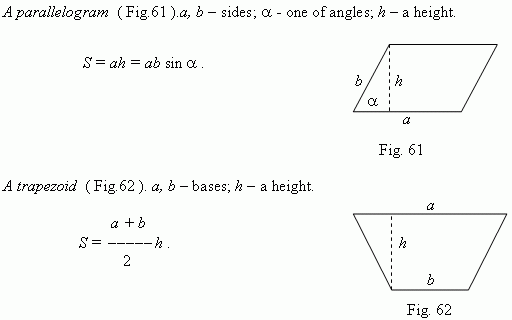
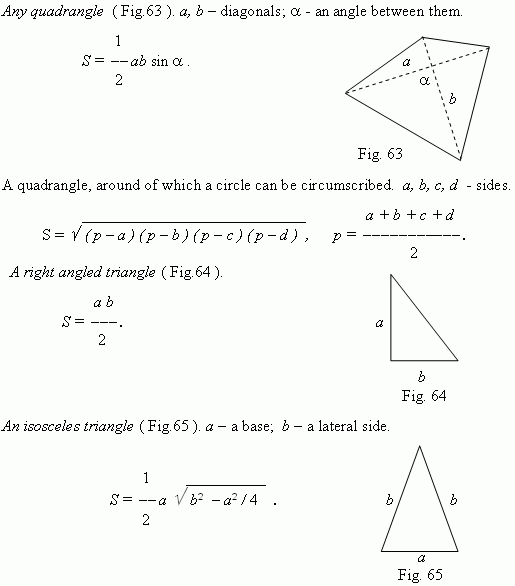
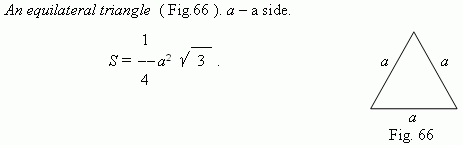
Any  triangle.  a, b, c – sides; a – a base; h – a height;  A, B, C – angles,
opposite to sides a, b, c ; p = ( a + b + c ) / 2.

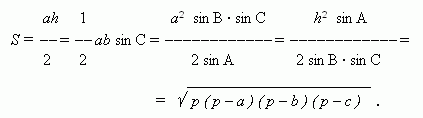
The last expression is known as Heron's formula.

A polygon, area of which we want to determine, can be divided into some triangles by its diagonals. A polygon, circumscribed around a circle  ( Fig. 67 ), can be divided by lines, going from a center of a circle to its vertices. Then we receive:

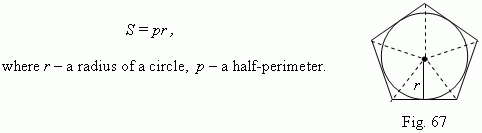
Particularly, this formula is valid for any regular polygon.

A regular hexagon.  a – a side .

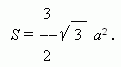
A circle. D – a diameter; r – a radius .

A sector ( Fig.68 ) .  r – a radius; n – a degree measure of a central angle;
l – a length of an arc.

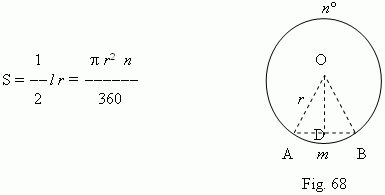
A segment ( Fig.68 ) . An area of a segment is found as a difference between areas of a sector A m BO and a triangle AOB. Besides, the approximate formula for an area of a segment is:

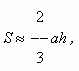
where a = AB ( Fig.68 ) – a base of segment; h – its height ( h = r – OD ). A relative error of this formula is equal:  at A m B = 60 deg  – about 1.5% ;  at  A m B = 30 deg   ~0.3%.

E x a m p l e .  Calculate areas of the sector A m BO  ( Fig.68 )  and the segment
A m B at the following data: r = 10 cm, n = 60 deg.

S o l u t i o n .  A sector area:

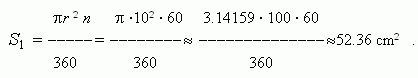
An area of the regular triangle AOB:

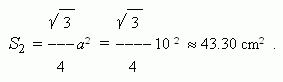
Hence, an area of a segment:

Note, that in a regular triangle AOB:  AB = AO = BO = r ,
AD = BD = r / 2 , and  therefore a height OD according to
Pythagorean theorem is equal to:

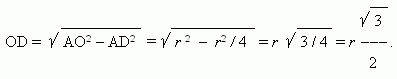
Then, according to the approximate formula we’ll receive: