Basic notions and properties of functions
Rule (law) of correspondence. Monotone function.
Bounded and unbounded function. Continuous and
discontinuous function. Even and odd function.
Periodic function. Period of a function.
Zeros (roots) of a function. Asymptote.
Domain and codomain of function.
In elementary mathematics we study functions only in a set of real numbers
R
. This means that an argument of a function can adopt only those real values, at which a function is defined, i.e. it also adopts only real values. A set
X
of all admissible real values of an argument
x
, at which a function
y
=
f
(
x
) is defined, is called a
domain of
a function
. A set
Y
of all real values
y
, that a function adopts, is called a
codomain of a function
. Now we can formulate a definition of a function more exactly:
such a rule (law) of a correspondence between a set
X
and
a set
Y
, that for each element of a set
X
one and only one element of a set
Y
can be found, is called a function
. From this definition it follows, that a function is given if :
- the domain of a function
X
is given;
- the codomain of a function
Y
is given;
- the correspondence rule ( law ), is known.
A correspondence rule must be such, that for
each value of an argument only one value
of a function
can be found. This requirement of a single-valued function is obligatory.
Monotone function. If for any two values of an argument x 1 and x 2 from the condition x 2 > x 1 it follows f ( x 2 ) > f ( x 1 ), then a function is called increasing ; if for any x 1 and x 2 from the condition x 2 > x 1 it follows f ( x 2 ) < f ( x 1 ), then a function is called decreasing .A function, which only increases or only decreases, is called a monotone function.
Bounded and unbounded functions.
A function is
bounded
, if such positive number
M
exists, that |
f
(
x
) |
M
for all values of
x .
If such positive number does not exist, then this function is
unbounded
.
E x a m p l e s.
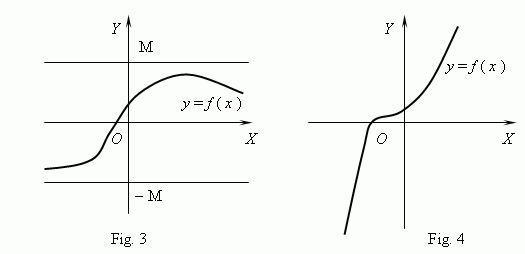
A function, shown on Fig.3, is a bounded, but not monotone function. On Fig.4 quite the opposite, we see a monotone, but unbounded function. ( Explain this, please ! ).
Continuous and discontinuous functions.
A function
y
=
f
(
x
) is called a
continuous
function at a point x
=
a,
if:
1) the function is defined at
x
=
a
, i.e.
f
(
a
) exists;
2) a
finite
lim
f
(
x
) exists;
x
→
a
( see
the paragraph "Limits of functions"
in the section “Principles of analysis”)
3)
f
(
a
) = lim
f
(
x
) .
x
→
a
If even one from these conditions isn’t executed, this function is called discontinuous at the point x = a .
If a function is continuous at all points of its domain, it is called a continuous function .
Even and odd functions.
If for
any
x
from a function domain:
f
( –
x
) =
f
(
x
), then this function is called
even
;
if
f
( –
x
) = –
f
(
x
), then this function is called
odd
. A graph of an even function is symmetrical relatively
y
-axis ( Fig.5 ), a graph of an odd function is symmetrical relatively the origin of coordinates ( Fig.6 ).
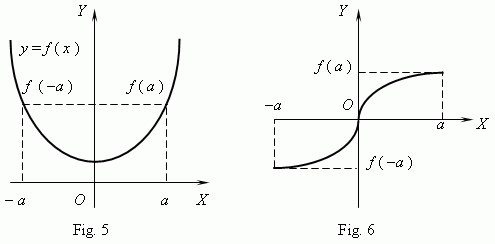
Periodic function.
A function
f
(
x
) is
periodic
, if such
non-zero
number
T
existsthat for
any
x
from a function domain:
f
(
x
+
T
) =
f
(
x
). The
least
such number is called a
period of a function
. All trigonometric functions are periodic.
E x a m p l e 1 . Prove that sin
x
has a number 2
as a period.
S o l u t i o n . We know, that sin (
x+
2
n
) = sin
x
, where
n
= 0, ± 1, ± 2, …
Hence, adding 2
n
to an argument of a sine doesn’t change its value.
Maybe another number with the such property exists ?
Assume, that
P
is the such number, i.e. the equality:
is valid for any value of x . Then this is valid for x =
/ 2 , i.e.
/ 2
+
P
) = sin
/ 2 = 1.
/ 2
+
P
) = cos
P
according to the reduction formula.Then from
the two last expressions it follows, that cos P = 1, but we know, that this
equality is right only if P = 2
n
. Because the least non-zero number of
2
n
is 2
, this is a period of sin
x
. It is proved analogously, that 2
is also
a period for cos x .
Prove, please, that functions tan x and cot x have
as a period.
E x a m p l e 2. What number is a period for the function sin 2
x
?
S o l u t i o n . Consider
n
) = sin [ 2 (
x
+
n
) ].
We see, that adding
n
to an argument
x
, doesn’t change the function value.
The least non-zero number of
n
is
, so this is a period of sin 2
x
.
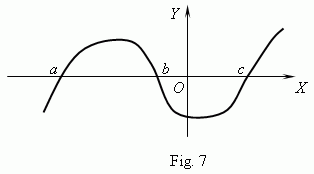
Zeros of function. An argument value, at which a function is equal to zero, is called a zero ( root ) of the function. It can be that a function has some zeros. For instance, the function y = x ( x + 1 ) ( x – 3) has the three zeros: x = 0, x = – 1, x = 3 . Geometrically, a zero of a function is x -coordinate of a point of intersection of the function graph and x -axis. On Fig.7 a graph of a function with zeros x = a , x = b and x = c is represented.
Asymptote. If a graph of a function unboundedly approaches to some straight line at itstaking off an origin of coordinates, then this straight line is called an asymptote .