Plane
General equation of plane. Normal vector.
Equation of plane in segments on axes.
Equation of plane going through the given point
and perpendicular to the given vector.
Parametric equation of plane.
Parallelism condition of planes.
Perpendicularity condition of planes.
Distance between two points .
Distance from point to plane.
Distance between parallel planes.
Angle between planes.
A general equation of plane:
Àõ + Âó + Ñ z + D = 0 ,
where À , B and C aren't equal to zero simultaneously.
Coefficients À , B and C are coordinates of normal vector of the plane ( i.e. vector, perpendicular to the plane ).
At
À
0,
Â
0,
Ñ
0 and
D
0
we receive
an
equation of plane in segments
on
axes
:
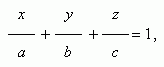
where a = – D / A , b = – D / B , c = – D / C . This plane goes through the points ( a , 0, 0 ), ( 0, b , 0 ) and ( 0, 0, ñ ), i.e. it cuts off segments a , b and c long on the coordinate axes.
An equation of plane , going through a point ( õ 0 , ó 0 , z 0 ) and perpendicular to a vector ( À , Â , C ) :
À ( õ – õ 0 ) + Â ( ó – ó 0 ) + Ñ ( z – z 0 ) = 0 .
A parametric equation of plane , passing through a point ( õ 0 , ó 0 , z 0 ) and two noncollinear vectors ( a 1 , b 1 , c 1 ) and ( a 2 , b 2 , c 2 ) , set in a rectangular cartesian system of soordinates:
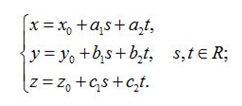
A parallelism condition of planes Àõ + Âó + Ñ z+ D = 0 and E õ + F ó + Gz+ H = 0 :
AF – BE = BG – CF = AG – CE = 0 .
A perpendicularity condition of planes Àõ + Âó + Ñ z+ D = 0 and E õ + F ó + Gz+ H = 0 :
À E + Â F + Ñ G = 0 .
A distance between two points ( x 1 , y 1 , z 1 ) and ( x 2 , y 2 , z 2 ) :
A distance from a point ( õ 0 , ó 0 , z 0 ) to a plane Àõ + Âó + Ñ z + D = 0 :
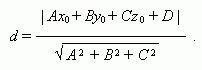
A distance between parallel planes Aõ + By + Cz + D = 0 and Aõ + By + Cz + Å = 0
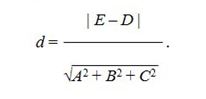
An angle
between planes
Àõ
+
Âó
+
Ñ
z+
D =
0
and
E
õ
+
F
ó
+
Gz+ H =
0 :
