Integral with variable upper limit of integration
Let
f
(
x
) be a continuous function, given in a
segment [
a
,
b
], then for any
x
[
a
,
b
] the function
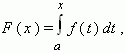
exists. This function is given as an integral with variable upper limit of integration in the right-hand part of the equality.
All rules and properties of a definite integral apply to an integral with variable upper limit of integration.
| E x a m p l e . |
A variable force acting on a linear way changes in the law:
f ( x ) = 6 x 2 + 5 at x 
0 . What law does a work of this force change in ?
|
| S o l u t i o n. |
A work of the force
f ( x
) on a segment [ 0 ,
x
] of linear way is equal to:
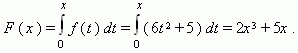
Thus, the work changes in the law: F ( x ) = 2 x 3 + 5 x . |
According to the definition of an
integral with variable upper limit of integration
or the
function
F
(
x
) and known properties of an integral it follows that at
x
[
a
,
b
]
F' ( x ) = f ( x ) .
Check this property using the above mentioned example.