Basic properties of derivatives and differentials

Properties of derivatives and differentials.
Derivative of a composite function.

If u ( x ) ≡ const , then

u’ ( x ) ≡ 0 , du ≡ 0.

If u ( x ) and v ( x ) are differentiable functions at a point x ₀ , then:

( c u ) ’ = c u’ , d ( c u ) = c du , ( c – const );

( u ± v ) ’ = u’ ± v’ , d ( u ± v ) = du ± dv ;

( u v ) ’ = u’ v + u v’ , d ( u v ) = v du + u dv ;

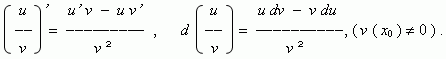
Derivative of a composite function. Consider a composite function, argument of which is also a function: h ( x ) = g ( f ( x ) ). If a function f has a derivative at a point x ₀ , and a function g has a derivative at a point f ( x ₀ ), then a composite function h has also a derivative at a point x ₀ , calculated by the formula:

h’ ( x ₀ ) = g’ ( f ( x ₀ ) ) · f’ ( x ₀ ) .

Back