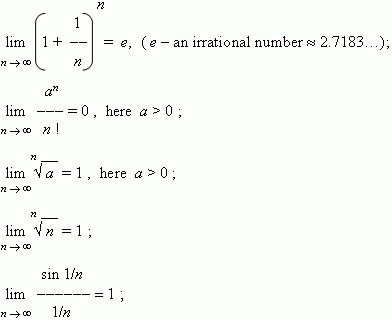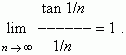Sequences. Limits of numerical sequences. Some remarkable limits
General term formula. Limit of numerical sequence.
Convergent sequence. Divergent sequence. Bounded sequence.
Monotone sequence. Weierstrass's theorem.
Basic properties of limits. Some remarkable limits.
Sequences.
Consider the series of natural numbers: 1, 2, 3, … ,
n
–1,
n
, … .
If to change each natural number
n
in this series by some number
u
n
, following
to some law, we’ll receive a new series of numbers:
and called a numerical sequence .
A value u n is called a general term of a sequence. Usually a numerical sequence is given by some formula u n = f ( n ) , permitting to find any term of the sequence by its number n; this formula is called a general term formula. Note, that it is not always possible to give the numerical sequence by a general term formula; sometimes a sequence is given by description of its terms ( see below the last example).
E x a m p l e s of numerical sequences:
1, 2, 3, 4, 5, … - a series of natural numbers ;
2, 4, 6, 8, 10, … - a series of event numbers;
1.4, 1.41, 1.414, 1.4142, …
- a numerical sequence of approximate,
defined more precisely values of
For the last sequence it is impossible to give a general term formula,
nevertheless this sequence is described
completely.
Limit of numerical sequence. Consider a numerical sequence, a general term of which approaches to some number a at increasing an ordinal number n . In this case we say, that the numerical sequence has a limit . This notation has a more strict definition: A number a is called a limit of a numerical sequence { u n } :
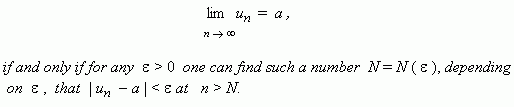
This definition means, that
a
is a
limit
of a numerical sequence, if its general term approaches unrestrictedly to
a
at increasing
n
.
Geometrically it means, that for any
> 0 it’s possible to find such a number
N
, that beginning from
n
>
N all
terms of the sequence are placed within an interval (
a
–
,
a
+
). A sequence,
having a limit, is called
convergent
; otherwise - a
divergent
sequence. A sequence is
bounded
, if such a number
M
exists that |
u
n
|
M
for all
n.
Increasing and decreasing sequences are called
monotone
sequences.
Weierstrass’s theorem. Each monotone and bounded sequence has a limit ( this theorem is used in a high school without a proof ).
Basic properties of limits. The below mentioned properties of limits are valid not only for numerical sequences, but also for functions.
If {
u
n
} and {
v
n
}
-
two convergent sequences, then:
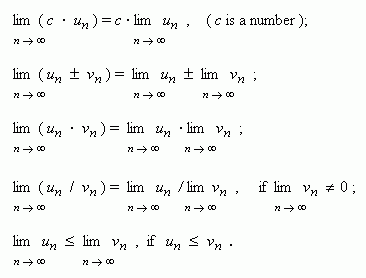
If terms of sequences {
u
n
}, {
v
n
},
{
w
n
}
satisfy the inequalities
u
n
v
n
w
n
and
lim
u
n
= lim
w
n
=
a
,
then lim
v
n
=
a .
Some remarkable limits.
