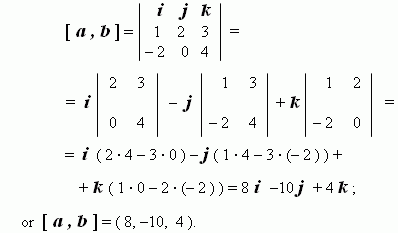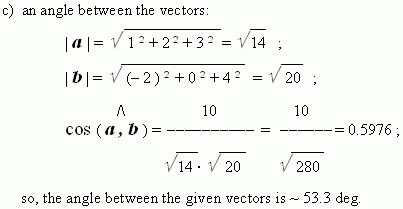Principles of vector calculus
Collinear vectors. Coplanar vectors. Equality of vectors. Parallel
transfer of vectors. Addition of vectors. Subtraction of vectors.
Laws of addition of vectors. Laws of multiplication of vector by a
number. Scalar product of vectors. Angle between non-zero vectors.
Scalar square. Properties of a scalar product. Unit orthogonal vectors.
Coordinates of a vector. Algebraic operations with vectors. Vector
product of vectors. Properties of a vector product. Necessary and
sufficient condition of collinearity of vectors. Necessary and sufficient
condition of coplanarity of vectors.
Vector is a directed segment, connecting two points in a space ( in a plane ). Vectors are signed usually eitherby small letters or by initial and final points. For example, a vector directed from point A to point B can be signed a s a ,
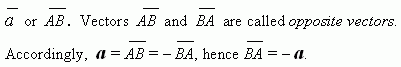
__
A zero vector 0 or 0 is avector, for which initial and final points coincide, i.e. A=B . From here it follows: 0 = – 0 .
A length ( modulus ) of vector a , signed as | a | , is a length of its imaging segment AB . Particularly, | 0 | = 0.
Vectors are called collinear ones, if their directed segments belong to parallel lines. Collinear vectors a and b are signed as a || b .
Three or more vectors are called coplanar , if they lie in the same plane.
Equality of vectors. Two vectors a and b are equal , if they are collinear ones and their lengths are equal , i.e. a || b and | a | = | b | . Hence, vectors don’t change ata parallel transfer.
Addition of vectors. As vectors are directed segments , then their addition can be executed geometrically. (Algebraic addition of vectors see below, in the point “Unit orthogonal vectors”).
Assume, that __ __
a = AB and b = CD ,
then __ __
a + b = AB + CD
is a vector, received after executing of the two operations:
a ) a parallel transfer of one of thevectors till its initial point will coincide with
a final point of another vector;
b ) a geometrical addition by drawing the resulting vector from an initial point
of an immovable vector to a final point of a transferred vector.
Subtraction of vectors. This operation is reduced to the previous by changing a subtracted vector to an oppositeone:
a
–
b
=
a
+
(
–
b
) .
Laws of addition. I. a + b = b + a ( C o m m u t a t i v i t y ).
II. ( a + b ) + c = a + ( b + c ) ( A s s o c i a t i v i t y ).
III. a + 0 = a .
IV. a + ( – a ) = 0 .
Laws of multiplication of vector by a number.
I. 1 · a = a , 0 · a = 0 , m · 0 = 0 , ( – 1 ) · a = – a .
II. m a = a m , | m a | = | m | · | a | .
III. m ( n a ) = ( m n ) a . ( A s s o c i a t i v i t y of
multiplication by a number ).
IV. ( m + n ) a = m a + n a , ( D i s t r i b u t i v i t y of
m ( a + b ) = m a + m b . multiplication by a number ).
__ __
Scalar product of vectors. Anangle between non-zero vectors AB and CD is an angle, formed at a parallel transfer one of the vectors till coinciding the points A and C. A scalarproduct of vectors a and b is called a number, equal to a product of lengths ( modules )of these vectors by cosine of angle between them:
![]()
If one of vectors is a zero vector, then a scalar product of these vectors is equal to zero by the definition:
( a , 0 ) = ( 0 , b ) = 0 .
If both vectors are non-zero ones, then cosine of the angle between them may be found by the formula:
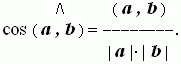
A scalar product ( a , a ), equal to | a | ² , is called a scalar square.
A length of vector a and its scalar square are tied by the relation:
![]()
A scalar product of two vectors is:
- positive , if an angle between the vectors is acute ;
- negative, if an angle between the vectors is obtuse .
A scalar product of two non-zero vectors is equal to zero , if and only if an angle between the vectors is right, i.e. these vectors are perpendicular ( orthogonal ):
![]()
Properties of a scalar product. For any vectors a , b , c and any number m the following relations are valid:
I. ( a , b ) = ( b , a ) . ( Co m m u t a t i v i t y )
II. ( m a , b ) = m ( a , b ) .
III. ( a + b , c ) = ( a , c ) + ( b , c ) . ( D i s t r i b u t i v i ty )
Unit orthogonal vectors. In anyrectangular system of coordinates it is possible to introduce unit two-and-two orthogonal vectors i , j and k , connected with coordinate axes: i – for x -axis, j – for y -axis and k – for z -axis. According to this definition we have:
( i , j ) = ( i , k ) = ( j , k ) = 0,
| i | = | j | = | k | = 1.
Any vector a can be expressed through these vectors by the only way: a = x i + y j + z k . Another form of the record is: a = ( x, y, z ) . Here x , y , z – coordinates of the vector a in this system of coordinates. According to the last relationand properties of the unit orthogonal vectors i , j , k a scalar product of two vectors can be written in another shape. Assume a = ( x, y, z ) ; b = ( u, v, w ) . Then ( a , b ) = xu + yv + zw . A scalar product of two vectors is equal to a sum of products of corresponding coordinates. A length (modulus) of vector a = ( x , y , z ) is equal to:
![]()
Besides, we receive now the possibility for algebraic operations with vectors; namely, addition and subtraction of vectors can be executed by coordinates:
a + b = ( x + u , y + v , z + w ) ;
a – b = ( x – u , y – v , z – w ) .
Vector product of vectors. A vector product [ a , b ] of vectors a and b ( in the indicated order ) is a vector:
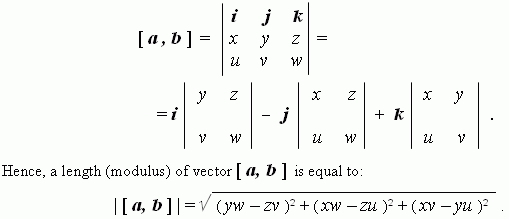
There is another formula for a length of vector
[
a, b
]
:
/\
| [ a, b ] | = | a | | b | sin ( a, b ) ,
i.e. a length ( modulus ) of vector product of the vectors a and b is equal to product of lengths ( modules )of these vectors by sine of the angle between them. Differently this fact can be interpreted as following : a length ( modulus ) of vector [ a, b ] is equal numerically to an area of parallelogram,built on vectors a and b .
Properties of vector product.
I. A vector [ a, b ] is perpendicular (orthogonal) both to vector a and vector b . ( Prove this, please ! ) .
II. [ a , b ] = – [ b , a ] . ( A n t i c o m m u t a t i v i t y ).
III. [ m a , b ] = m [ a , b ] .
IV. [ a + b , c ] = [ a , c ] + [ b , c ] . ( D i s t r i b u t i v i t y ).
V. [ a , [ b , c ] ] = b ( a , c ) – c ( a , b ) .
VI. [ [ a , b ] , c ] = b ( a , c ) – a ( b , c ) .
Necessaryand sufficient condition of collinearity of vectors a = ( x, y, z ) and b = ( u, v, w ) :
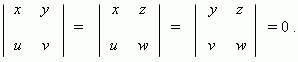
Necessary and sufficient condition of coplanarity
of vectors
a
=
(
x, y, z
)
,
b
=
(
u, v, w
) and
c
=
(
p, q, r
) :
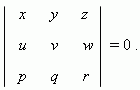
E x a m p l e . The vectors:
a
= ( 1, 2, 3 ) and
b
= ( – 2 , 0 ,4 ) are given. Calculate
their scalar product, vector product and an angle between these vectors.
S o l u t i o n . Using the corresponding formulas (see above), we’ll receive:
a). the scalar product: ( a , b ) = 1 · ( – 2 ) + 2 · 0 + 3 · 4 = 10 ;
b). the vector product: