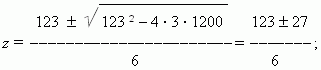Equations of higher degrees

Equations of higher degrees.
Biquadratic equation. Cubic equation.

1. Some kinds of the higher degrees equations may be solved using a quadratic equation. Sometimes one can resolve the left-hand side of equation to factors, each of them is a polynomial of the degree not higher than second. Then, equaling each of them to zero and solving all these quadratic and / or linear equations,  we’ll receive all roots of the original equation.

E x a m p l e .  Solve an equation:  3 x 4 + 6 x 3 – 9 x 2 = 0 .

S o l u ti o n .  Resolve the left-hand side of this equation to factors:

x 2 ( 3 x 2 +  6 x –  9 ) .

Solve the equation: x 2 = 0; it has two equal roots: x 1 = x 2 = 0 .
Now we solve the equation: 3 x 2 +  6 x – 9 = 0,  and receive:
x 3 = 1  and x 4 = – 3 . Thus,  the original equation has four roots:
x 1 = x 2 = 0 ; x 3 = 1 ; x 4 = – 3 .

2. If an equation has the shape:

ax 2 n + bx n +  c = 0  ,

it is reduced to an quadratic equation by the exchange:

x n = z ;

really, after this exchange we receive: az 2 + bz + c = 0 .

E x a m p l e .  Consider the equation:

x 4 – 13 x 2 + 36 = 0 .

Exchange: x 2 = z . After this we receive:

z 2 – 13 z + 36 = 0 .

Its roots are: z 1 = 4  and z 2 = 9. Now we solve the equations:

x 2 = 4 and x 2 = 9 . They have the roots correspondingly:

x 1 = 2  , x 2 = – 2 , x 3 = 3 ; x 4 = – 3 .  These numbers are

the roots of the original equation ( check this, please ! ).

Any equation of the shape:  ax 4 + bx 2 +  c = 0 is called a biquadratic equation. It is reduced to quadratic equations by using the exchange: x 2 = z .

E x a m p l e .  Solve the biquadratic equation:  3 x 4 – 123 x 2 + 1200 = 0 .

S o l u t i o n .  Exchanging: x 2 = z , and solving the equation:

3 z 2 – 123 z + 1200 = 0 , we’ll receive:

hence, z 1 = 25  and z 2 = 16 . Using our exchange, we receive:

x 2 = 25 and x 2 = 16, hence, x 1 = 5, x 2 = –5, x 3 = 4, x 4 = – 4.

3. A cubic equation is the third degree equation; its general shape is:

ax 3 + bx 2 + cx + d = 0 .

The known Cardano’s formulas for solution of this kind equations are very difficult and almost aren’t used in practice. So, we recommend  another way to solve the third degree equations.
1). At first we find one root of the equation by selecting, because these equations have always at least one real root , and an integer root of a cubic equation with integer coefficients is one of factors of a free term d. Coefficients of these equations have been selected usually so that the root, which must be found, is among not great integers, such as: 0, ± 1, ± 2, ± 3. Therefore, we’ll find the root among these numbers and check it by substituting into the equation. A probability of successful result is very high. Assume this root is x 1 .
2). The second stage of solution is dividing of the third degree polynomial ax 3 + bx 2 + cx + d by the binomial  ( x – x 1 ) . A ccording to Bezout’s theorem (see the section “Division of polynomial by linear binomial”) this division is possible without a remainder, and we’ll receive as a result the second degree polynomial, which would be annihilated, will give us a quadratic equation, solving which we’ll find (or not !) the rest of the two  roots.

E x a m p l e .  Solve the equation: x 3 – 3 x 2 – 13 x + 15 = 0 .

S o l u t i o n .  Selecting the first root among the indicated numbers:

–2 ,  –1,  0,  1,  2  and substituting each of them in the

given equation, we find that  1  is a root of this equation.

Dividing  the left-hand side of the equation by binomial

( x – 1 ), we’ll receive:

Now we solve a quadratic equation: x 2 – 2 x – 15 = 0

find the rest of the two roots: x 1 = – 3  and x 2 = 5 .

Back