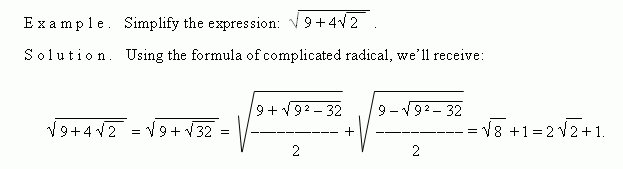Irrational numbers . Formula of complicated radical

Rational numbers. Irrational numbers.
Examples of irrational numbers.
Formula of complicated radical.

Irrational numbers in contrast to rational numbers (see above) aren’t presented as a vulgar, not cancelled fraction of the shape: m / n , where m and n are integers. There are numbers of a new kind , which are calculated with any accuracy, but can’t be changed by a rational number. They can appear as results of geometrical measurements, for example:

- a ratio of a square diagonal length to its side length is equal to ,

- a ratio of a circumference length to its diameter length is an irrational number

Examples of another irrational numbers:

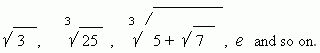
Let's prove that is the irrational number. Assume the opposite: is the rational number, then according to the definition of rational number we can write: = m / n , then: 2 = m ² / n ² , hence , m ² = 2 n ² , that is m ² is divisible by 2, hence, m is divisible by 2 and it is possible to write: m = 2 k , then m ² = 4 k ² or 4 k ² = 2 n ² , hence, n ² = 2 k ² , that is n ² is divisible by 2, then n is divisible by 2, hence, m è n have the common factor 2, what contradicts to the definition of rational number (see above). So, we have proved that is the irrational number.

To realize algebraic transformations of irrational expressions and equations,

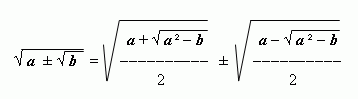
containing square roots, the following formula of complicated radical

may be useful (all the radicands are nonnegative). To prove the formula it is enough to raise to square the both of its parts.

Back