Powers and roots
Power of product of some factors. Power of a quotient (fraction). Raising of power to a power. Operations with roots. Arithmetical
root. Root of product of some factors. Root of quotient (fraction).
Raising of root to a power. Proportional change of degrees of a
root and its radicand. Negative, zero and fractional exponents
of a power. About meaningless expressions.
Operations with powers.
1. At multiplying of powers with the same base their exponents are added:
a m · a n = a m + n .
2. At dividing of powers with the same base their exponents are subtracted:
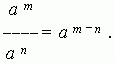
3. A power of product of two or some factors is equal to a product of powers of these factors:
( abc … ) n = a n · b n · c n …
4. A power of a quotient (fraction) is equal to a quotient of powers of a dividend (numerator) and a divisor (denominator):
( a / b ) n = a n / b n .
5. At raising of a power to a power their exponents are multiplied:
( a m ) n = a m n .
All above mentioned formulas are read and executed in both directions – from the left to the right and back.
E x a m p l e . ( 2 · 3 · 5 / 15 ) 2 = 2 2 · 3 2 · 5 2 / 15 2 = 900 / 225 = 4 .
Operations with roots.
In all below mentioned formulas
a symbol
means an
arithmetical root
(
all radicands are considered here only positive
).
1. A root of product of some factors is equal to a product of roots of these factors:
2. A root of a quotient is equal to a quotient of roots of a dividend and a divisor:
3. At raising a root to a power it is sufficient to raise a radicand to this power:
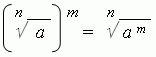
4. If to increase a degree of a root by m times and to raise simultaneously its radicand to the m -th power, the root value doesn’t change:
5. If to decrease a degree of a root by m times and to extract simultaneously the m -th degree root of the radicand, the root value doesn’t change:
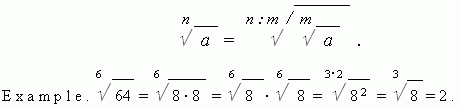
Widening of the power notion. Till now we considered only natural exponents of powers; but operations with powers and roots can result also to negative , zero and fractional exponents . All these exponents of powers require to be defined.
Negative exponent of a power. A power of some number with a negative (integer) exponent is defined as unit divided by the power of the same number with the exponent equal to an absolute value of the negative exponent:
Now the formula a m : a n = a m - n may be used not only if m is more than n , but also for a case if m is less than n .
E x a m p l e . a 4 : a 7 = a 4 - 7 = a - 3 .
If we want the formula a m : a n = a m - n to be valid at m = n we need the definition of zero exponent of a power.
Zero exponent of a power. A power of any non-zero number with zero exponent is equal to 1.
E x a m p l e s . 2 0 = 1, ( – 5 ) 0 = 1, ( – 3 / 5 ) 0 = 1.
Fractional exponent of a power. To raise a real number a to a power with an exponent m / n it is necessary to extract the n -th degree root from the m -th power of this number a :
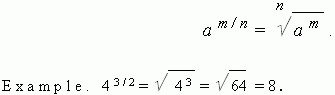
About meaningless expressions. There are some expressions:
Case 1.
where
a
≠
0
,
doesn’t exist
.
Really, if to assume that
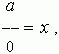where
x
– some number, then according
to the definition of a division we have: a = 0 · x , i.e. a = 0 , but this result
contradicts to the condition: a ≠ 0 .
Case 2.
is
any number.
Really, if to assume that this expression is equal to some number x , then
according to the definition of a division: 0 = 0 · x . But this equality is valid
at any number x , which was to be proved.
Case 3.
If to assume, that rules of operations with powers are spread to powers with
a zero base, then
0 0 is any number .
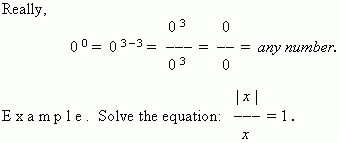
S o l u t i o n . Consider the three main cases:
1) x = 0 – this value doesn’t satisfy the equation ( Why ? ) ;
2) at x > 0 we receive: x / x = 1, i.e.1 = 1, hence, x – any number,
but taking into consideration that in this case x > 0, the answer
is: x > 0 ;
3) at x < 0 we receive: – x / x = 1, i.e. –1 = 1, and the answer is:
there is no solution in this case.
So, the answer: x > 0 .